9. Sequential Data Types
By Bernd Klein. Last modified: 29 Jun 2022.
Introduction
Sequences are one of the principal built-in data types besides numerics, mappings, files, instances and exceptions. Python provides for six sequence (or sequential) data types:
strings
byte sequences
byte arrays
lists
tuples
range objects
Strings, lists, tuples, bytes and range objects may look like utterly different things, but they still have some underlying concepts in common:
The items or elements of strings, lists and tuples are ordered in a defined sequence
The elements can be accessed via indices
text = "Lists and Strings can be accessed via indices!"
print(text[0], text[10], text[-1])
OUTPUT:
L S !
Accessing lists:
cities = ["Vienna", "London", "Paris",
"Berlin", "Zurich", "Hamburg"]
print(cities[0])
print(cities[2])
print(cities[-1])
OUTPUT:
Vienna Paris Hamburg
Unlike other programming languages Python uses the same syntax and function names to work on sequential data types. For example, the length of a string, a list, and a tuple can be determined with a function called len():
countries = ["Germany", "Switzerland", "Austria",
"France", "Belgium", "Netherlands",
"England"]
len(countries) # the length of the list, i.e. the number of objects
OUTPUT:
7
fib = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
len(fib)
OUTPUT:
10
Live Python training
See our Python training courses
Bytes
The byte object is a sequence of small integers. The elements of a byte object are in the range 0 to 255, corresponding to ASCII characters and they are printed as such.
s = "Glückliche Fügung"
s_bytes = s.encode('utf-8')
s_bytes
OUTPUT:
b'Gl\xc3\xbcckliche F\xc3\xbcgung'
Python Lists
So far we had already used some lists, and here comes a proper introduction. Lists are related to arrays of programming languages like C, C++ or Java, but Python lists are by far more flexible and powerful than "classical" arrays. For example, not all the items in a list need to have the same type. Furthermore, lists can grow in a program run, while in C the size of an array has to be fixed at compile time.
Generally speaking a list is a collection of objects. To be more precise: A list in Python is an ordered group of items or elements. It's important to notice that these list elements don't have to be of the same type. It can be an arbitrary mixture of elements like numbers, strings, other lists and so on. The list type is essential for Python scripts and programs, in other words, you will hardly find any serious Python code without a list.
The main properties of Python lists:
- They are ordered
- The contain arbitrary objects
- Elements of a list can be accessed by an index
- They are arbitrarily nestable, i.e. they can contain other lists as sublists
- Variable size
- They are mutable, i.e. the elements of a list can be changed
List Notation and Examples
List objects are enclosed by square brackets and separated by commas. The following table contains some examples of lists:
| List | Description |
|---|---|
[] |
An empty list |
[1,1,2,3,5,8] |
A list of integers |
[42, "What's the question?", 3.1415] |
A list of mixed data types |
["Stuttgart", "Freiburg", "München", "Nürnberg", "Würzburg", "Ulm","Friedrichshafen", Zürich", "Wien"] |
A list of Strings |
[["London","England", 7556900], ["Paris","France",2193031], ["Bern", "Switzerland", 123466]] |
A nested list |
["High up", ["further down", ["and down", ["deep down", "the answer", 42]]]] |
A deeply nested list |
Accessing List elements
Assigning a list to a variable:
languages = ["Python", "C", "C++", "Java", "Perl"]
There are different ways of accessing the elements of a list. Most probably the easiest way for C programmers will be through indices, i.e. the numbers of the lists are enumerated starting with 0:
languages = ["Python", "C", "C++", "Java", "Perl"]
print(languages[0] + " and " + languages[1] + " are quite different!")
print("Accessing the last element of the list: " + languages[-1])
OUTPUT:
Python and C are quite different! Accessing the last element of the list: Perl
The previous example of a list has been a list with elements of equal data types. But as we saw before, lists can have various data types, as shown in the following example:
group = ["Bob", 23, "George", 72, "Myriam", 29]
Sublists
Lists can have sublists as elements. These sublists may contain sublists as well, i.e. lists can be recursively constructed by sublist structures.
person = [["Marc", "Mayer"],
["17, Oxford Str", "12345", "London"],
"07876-7876"]
name = person[0]
print(name)
OUTPUT:
['Marc', 'Mayer']
first_name = person[0][0]
print(first_name)
OUTPUT:
Marc
last_name = person[0][1]
print(last_name)
OUTPUT:
Mayer
address = person[1]
print(address)
OUTPUT:
['17, Oxford Str', '12345', 'London']
street = person[1][0]
print(street)
OUTPUT:
17, Oxford Str
We could have used our variable address as well:
street = address[0]
print(street)
OUTPUT:
17, Oxford Str
The next example shows a more complex list with a deeply structured list:
complex_list = [["a", ["b", ["c", "x"]]]]
complex_list = [["a", ["b", ["c", "x"]]], 42]
complex_list[0][1]
OUTPUT:
['b', ['c', 'x']]
complex_list[0][1][1][0]
OUTPUT:
'c'
Live Python training
See our Python training courses
Changing list
languages = ["Python", "C", "C++", "Java", "Perl"]
languages[4] = "Lisp"
languages
OUTPUT:
['Python', 'C', 'C++', 'Java', 'Lisp']
languages.append("Haskell")
languages
OUTPUT:
['Python', 'C', 'C++', 'Java', 'Lisp', 'Haskell']
languages.insert(1, "Perl")
languages
OUTPUT:
['Python', 'Perl', 'C', 'C++', 'Java', 'Lisp', 'Haskell']
shopping_list = ['milk', 'yoghurt', 'egg', 'butter', 'bread', 'bananas']
We go to a virtual supermarket. Fetch a cart and start shopping:
shopping_list = ['milk', 'yoghurt', 'egg', 'butter', 'bread', 'bananas']
cart = []
# "pop()"" removes the last element of the list and returns it
article = shopping_list.pop()
print(article, shopping_list)
cart.append(article)
print(cart)
# we go on like this:
article = shopping_list.pop()
print("shopping_list:", shopping_list)
cart.append(article)
print("cart: ", cart)
OUTPUT:
bananas ['milk', 'yoghurt', 'egg', 'butter', 'bread'] ['bananas'] shopping_list: ['milk', 'yoghurt', 'egg', 'butter'] cart: ['bananas', 'bread']
With a while loop:
shopping_list = ['milk', 'yoghurt', 'egg', 'butter', 'bread', 'bananas']
cart = []
while shopping_list != []:
article = shopping_list.pop()
cart.append(article)
print(article, shopping_list, cart)
print("shopping_list: ", shopping_list)
print("cart: ", cart)
OUTPUT:
bananas ['milk', 'yoghurt', 'egg', 'butter', 'bread'] ['bananas'] bread ['milk', 'yoghurt', 'egg', 'butter'] ['bananas', 'bread'] butter ['milk', 'yoghurt', 'egg'] ['bananas', 'bread', 'butter'] egg ['milk', 'yoghurt'] ['bananas', 'bread', 'butter', 'egg'] yoghurt ['milk'] ['bananas', 'bread', 'butter', 'egg', 'yoghurt'] milk [] ['bananas', 'bread', 'butter', 'egg', 'yoghurt', 'milk'] shopping_list: [] cart: ['bananas', 'bread', 'butter', 'egg', 'yoghurt', 'milk']
Tuples
A tuple is an immutable list, i.e. a tuple cannot be changed in any way, once it has been created. A tuple is defined analogously to lists, except the set of elements is enclosed in parentheses instead of square brackets. The rules for indices are the same as for lists. Once a tuple has been created, you can't add elements to a tuple or remove elements from a tuple.
Where is the benefit of tuples?
•Tuples are faster than lists.
•If you know that some data doesn't have to be changed, you should use tuples instead of lists, because this protects your data against accidental changes.
•The main advantage of tuples is that tuples can be used as keys in dictionaries, while lists can't.
The following example shows how to define a tuple and how to access a tuple. Furthermore, we can see that we raise an error, if we try to assign a new value to an element of a tuple:
t = ("tuples", "are", "immutable")
t[0]
OUTPUT:
'tuples'
t[0] = "assignments to elements are not possible"
OUTPUT:
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-13-fa4ace6c4d57> in <module> ----> 1 t[0]="assignments to elements are not possible" TypeError: 'tuple' object does not support item assignment
Live Python training
See our Python training courses
Slicing
In many programming languages it can be quite tough to slice a part of a string and even harder, if you like to address a "subarray". Python makes it very easy with its slice operator. Slicing is often implemented in other languages as functions with possible names like "substring", "gstr" or "substr".
So every time you want to extract part of a string or a list in Python, you should use the slice operator. The syntax is simple. Actually it looks a little bit like accessing a single element with an index, but instead of just one number, we have more, separated with a colon ":". We have a start and an end index, one or both of them may be missing. It's best to study the mode of operation of slice by having a look at examples:
slogan = "Python is great"
first_six = slogan[0:6]
first_six
OUTPUT:
'Python'
starting_at_five = slogan[5:]
starting_at_five
OUTPUT:
'n is great'
a_copy = slogan[:]
without_last_five = slogan[0:-5]
without_last_five
OUTPUT:
'Python is '
Syntactically, there is no difference on lists. We will return to our previous example with European city names:
cities = ["Vienna", "London", "Paris", "Berlin", "Zurich", "Hamburg"]
first_three = cities[0:3]
# or easier:
...
first_three = cities[:3]
print(first_three)
OUTPUT:
['Vienna', 'London', 'Paris']
Now we extract all cities except the last two, i.e. "Zurich" and "Hamburg":
all_but_last_two = cities[:-2]
print(all_but_last_two)
OUTPUT:
['Vienna', 'London', 'Paris', 'Berlin']
Slicing works with three arguments as well. If the third argument is for example 3, only every third element of the list, string or tuple from the range of the first two arguments will be taken.
If s is a sequential data type, it works like this:
s[begin: end: step]
The resulting sequence consists of the following elements:
s[begin], s[begin + 1 * step], ... s[begin + i * step] for all (begin + i * step) < end.
In the following example we define a string and we print every third character of this string:
slogan = "Python under Linux is great"
slogan[::3]
OUTPUT:
'Ph d n e'
The following string, which looks like a letter salad, contains two sentences. One of them contains covert advertising of my Python courses in Canada:
"TPoyrtohnotno ciosu rtshees lianr gTeosrto nCtiot yb yi nB oCdaennasdeao"
Try to find out the hidden sentence using Slicing. The solution consists of 2 steps!
s = "TPoyrtohnotno ciosu rtshees lianr gTeosrto nCtiot yb yi nB oCdaennasdeao"
print(s)
OUTPUT:
TPoyrtohnotno ciosu rtshees lianr gTeosrto nCtiot yb yi nB oCdaennasdeao
s[::2]
OUTPUT:
'Toronto is the largest City in Canada'
s[1::2]
OUTPUT:
'Python courses in Toronto by Bodenseo'
You may be interested in how we created the string. You have to understand list comprehension to understand the following:
s = "Toronto is the largest City in Canada"
t = "Python courses in Toronto by Bodenseo"
s = "".join(["".join(x) for x in zip(s,t)])
s
OUTPUT:
'TPoyrtohnotno ciosu rtshees lianr gTeosrto nCtiot yb yi nB oCdaennasdeao'
Length

Length of a sequence, i.e. a list, a string or a tuple, can be determined with the function len(). For strings it counts the number of characters, and for lists or tuples the number of elements are counted, whereas a sublist counts as one element.
txt = "Hello World"
len(txt)
OUTPUT:
11
a = ["Swen", 45, 3.54, "Basel"]
len(a)
OUTPUT:
4
Live Python training
See our Python training courses
Concatenation of Sequences
Combining two sequences like strings or lists is as easy as adding two numbers together. Even the operator sign is the same. The following example shows how to concatenate two strings into one:
firstname = "Homer"
surname = "Simpson"
name = firstname + " " + surname
print(name)
OUTPUT:
Homer Simpson
It's as simple for lists:
colours1 = ["red", "green","blue"]
colours2 = ["black", "white"]
colours = colours1 + colours2
print(colours)
OUTPUT:
['red', 'green', 'blue', 'black', 'white']
The augmented assignment "+=" which is well known for arithmetic assignments work for sequences as well.
s += t
is syntactically the same as:
s = s + t
But it is only syntactically the same. The implementation is different: In the first case the left side has to be evaluated only once. Augment assignments may be applied for mutable objects as an optimization.
Checking if an Element is Contained in List
It's easy to check, if an item is contained in a sequence. We can use the "in" or the "not in" operator for this purpose. The following example shows how this operator can be applied:
abc = ["a","b","c","d","e"]
"a" in abc
OUTPUT:
True
"a" not in abc
OUTPUT:
False
"e" not in abc
OUTPUT:
False
"f" not in abc
OUTPUT:
True
slogan = "Python is easy!"
"y" in slogan
OUTPUT:
True
"x" in slogan
OUTPUT:
False
Live Python training
See our Python training courses
Repetitions
So far we had a "+" operator for sequences. There is a "*" operator available as well. Of course, there is no "multiplication" between two sequences possible. "*" is defined for a sequence and an integer, i.e. "s * n" or "n * s". It's a kind of abbreviation for an n-times concatenation, i.e.
str * 4
is the same as
str + str + str + str
Further examples:
3 * "xyz-"
OUTPUT:
'xyz-xyz-xyz-'
"xyz-" * 3
OUTPUT:
'xyz-xyz-xyz-'
3 * ["a","b","c"]
OUTPUT:
['a', 'b', 'c', 'a', 'b', 'c', 'a', 'b', 'c']
The augmented assignment for "*" can be used as well: s *= n is the same as s = s * n.
The Pitfalls of Repetitions
In our previous examples we applied the repetition operator on strings and flat lists. We can apply it to nested lists as well:
x = ["a","b","c"]
y = [x] * 4
y
OUTPUT:
[['a', 'b', 'c'], ['a', 'b', 'c'], ['a', 'b', 'c'], ['a', 'b', 'c']]
y[0][0] = "p"
y
OUTPUT:
[['p', 'b', 'c'], ['p', 'b', 'c'], ['p', 'b', 'c'], ['p', 'b', 'c']]
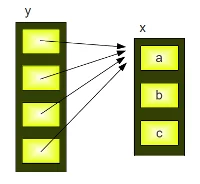
This result is quite astonishing for beginners of Python programming. We have assigned a new value to the first element of the first sublist of y, i.e. y[0][0] and we have "automatically" changed the first elements of all the sublists in y, i.e. y[1][0], y[2][0], y[3][0].
The reason is that the repetition operator "* 4" creates 4 references to the list x: and so it's clear that every element of y is changed, if we apply a new value to y[0][0].
