5. Numpy Arrays: Concatenating, Flattening and Adding Dimensions
By Bernd Klein. Last modified: 24 Mar 2022.
So far, we have learned in our tutorial how to create arrays and how to apply numerical operations on numpy arrays. If we program with numpy, we will come sooner or later to the point, where we will need functions to manipulate the shape or dimension of arrays. We wil also learn how to concatenate arrays. Furthermore, we will demonstrate the possibilities to add dimensions to existing arrays and how to stack multiple arrays. We will end this chapter by showing an easy way to construct new arrays by repeating existing arrays.
The picture shows a tesseract. A tesseract is a hypercube in $\Re^4$. The tesseract is to the cube as the cube is to the square: the surface of the cube consists of six square sides, whereas the hypersurface of the tesseract consists of eight cubical cells.
Flatten and Reshape Arrays
There are two methods to flatten a multidimensional array:
- flatten()
- ravel()
flatten
flatten is a ndarry method with an optional keyword parameter "order". order can have the values "C", "F" and "A". The default of order is "C". "C" means to flatten C style in row-major ordering, i.e. the rightmost index "changes the fastest" or in other words: In row-major order, the row index varies the slowest, and the column index the quickest, so that a[0,1] follows [0,0].
"F" stands for Fortran column-major ordering. "A" means preserve the the C/Fortran ordering.
import numpy as np
A = np.array([[[ 0, 1],
[ 2, 3],
[ 4, 5],
[ 6, 7]],
[[ 8, 9],
[10, 11],
[12, 13],
[14, 15]],
[[16, 17],
[18, 19],
[20, 21],
[22, 23]]])
Flattened_X = A.flatten()
print(Flattened_X)
print(A.flatten(order="C"))
print(A.flatten(order="F"))
print(A.flatten(order="A"))
OUTPUT:
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] [ 0 8 16 2 10 18 4 12 20 6 14 22 1 9 17 3 11 19 5 13 21 7 15 23] [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
ravel
The order of the elements in the array returned by ravel() is normally "C-style".
ravel(a, order='C')
ravel returns a flattened one-dimensional array. A copy is made only if needed.
The optional keyword parameter "order" can be 'C','F', 'A', or 'K'
'C': C-like order, with the last axis index changing fastest, back to the first axis index changing slowest. "C" is the default!
'F': Fortran-like index order with the first index changing fastest, and the last index changing slowest.
'A': Fortran-like index order if the array "a" is Fortran contiguous in memory, C-like order otherwise.
'K': read the elements in the order they occur in memory, except for reversing the data when strides are negative.
print(A.ravel())
print(A.ravel(order="A"))
print(A.ravel(order="F"))
print(A.ravel(order="A"))
print(A.ravel(order="K"))
OUTPUT:
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] [ 0 8 16 2 10 18 4 12 20 6 14 22 1 9 17 3 11 19 5 13 21 7 15 23] [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
reshape
The method reshape() gives a new shape to an array without changing its data, i.e. it returns a new array with a new shape.
reshape(a, newshape, order='C')
| Parameter | Meaning |
|---|---|
| a | array_like, Array to be reshaped. |
| newshape | int or tuple of ints |
| order | 'C', 'F', 'A', like in flatten or ravel |
X = np.array(range(24))
Y = X.reshape((3,4,2))
Y
OUTPUT:
array([[[ 0, 1],
[ 2, 3],
[ 4, 5],
[ 6, 7]],
[[ 8, 9],
[10, 11],
[12, 13],
[14, 15]],
[[16, 17],
[18, 19],
[20, 21],
[22, 23]]])
Live Python training
See our Python training courses
Concatenating Arrays
In the following example we concatenate three one-dimensional arrays to one array. The elements of the second array are appended to the first array. After this the elements of the third array are appended:
x = np.array([11,22])
y = np.array([18,7,6])
z = np.array([1,3,5])
c = np.concatenate((x,y,z))
print(c)
OUTPUT:
[11 22 18 7 6 1 3 5]
If we are concatenating multidimensional arrays, we can concatenate the arrays according to axis. Arrays must have the same shape to be concatenated with concatenate(). In the case of multidimensional arrays, we can arrange them according to the axis. The default value is axis = 0:
x = np.array(range(24))
x = x.reshape((3,4,2))
y = np.array(range(100,124))
y = y.reshape((3,4,2))
z = np.concatenate((x,y))
print(z)
OUTPUT:
[[[ 0 1] [ 2 3] [ 4 5] [ 6 7]] [[ 8 9] [ 10 11] [ 12 13] [ 14 15]] [[ 16 17] [ 18 19] [ 20 21] [ 22 23]] [[100 101] [102 103] [104 105] [106 107]] [[108 109] [110 111] [112 113] [114 115]] [[116 117] [118 119] [120 121] [122 123]]]
We do the same concatenation now with axis=1:
z = np.concatenate((x,y),axis = 1)
print(z)
OUTPUT:
[[[ 0 1] [ 2 3] [ 4 5] [ 6 7] [100 101] [102 103] [104 105] [106 107]] [[ 8 9] [ 10 11] [ 12 13] [ 14 15] [108 109] [110 111] [112 113] [114 115]] [[ 16 17] [ 18 19] [ 20 21] [ 22 23] [116 117] [118 119] [120 121] [122 123]]]
Adding New Dimensions
New dimensions can be added to an array by using slicing and np.newaxis. We illustrate this technique with an example:
x = np.array([2,5,18,14,4])
y = x[:, np.newaxis]
print(y)
OUTPUT:
[[ 2] [ 5] [18] [14] [ 4]]
Live Python training
Upcoming online Courses
23 Jun to 27 Jun 2025
28 Jul to 01 Aug 2025
08 Sep to 12 Sep 2025
20 Oct to 24 Oct 2025
04 Jun to 06 Jun 2025
30 Jul to 01 Aug 2025
10 Sep to 12 Sep 2025
22 Oct to 24 Oct 2025
Efficient Data Analysis with Pandas
02 Jun to 03 Jun 2025
23 Jun to 24 Jun 2025
28 Jul to 29 Jul 2025
08 Sep to 09 Sep 2025
20 Oct to 21 Oct 2025
04 Jun to 06 Jun 2025
10 Sep to 12 Sep 2025
22 Oct to 24 Oct 2025
See our Python training courses
Vector Stacking
A = np.array([3, 4, 5])
B = np.array([1,9,0])
print(np.row_stack((A, B)))
print(np.column_stack((A, B)))
np.shape(A)
OUTPUT:
[[3 4 5] [1 9 0]] [[3 1] [4 9] [5 0]] (3,)
A = np.array([[3, 4, 5],
[1, 9, 0],
[4, 6, 8]])
np.column_stack((A, A, A))
OUTPUT:
array([[3, 4, 5, 3, 4, 5, 3, 4, 5],
[1, 9, 0, 1, 9, 0, 1, 9, 0],
[4, 6, 8, 4, 6, 8, 4, 6, 8]])
np.column_stack((A[0], A[0], A[0]))
OUTPUT:
array([[3, 3, 3],
[4, 4, 4],
[5, 5, 5]])
np.dstack((A, A, A))
OUTPUT:
array([[[3, 3, 3],
[4, 4, 4],
[5, 5, 5]],
[[1, 1, 1],
[9, 9, 9],
[0, 0, 0]],
[[4, 4, 4],
[6, 6, 6],
[8, 8, 8]]])
Repeating Patterns, The "tile" Method
Sometimes, you want to or have to create a new matrix by repeating an existing matrix multiple times to create a new matrix with a different shape or even dimension. You may have for example a one-dimensional array array([ 3.4]) and you want to turn it into an array array([ 3.4, 3.4, 3.4, 3.4, 3.4])
In another usecase you may have a two-dimensional array like np.array([ [1, 2], [3, 4]]), which you intend to use as a building block to construe the array with the shape (6, 8):
array([[1, 2, 1, 2, 1, 2, 1, 2],
[3, 4, 3, 4, 3, 4, 3, 4],
[1, 2, 1, 2, 1, 2, 1, 2],
[3, 4, 3, 4, 3, 4, 3, 4],
[1, 2, 1, 2, 1, 2, 1, 2],
[3, 4, 3, 4, 3, 4, 3, 4]])
The idea of construction is depicted in the following diagram:
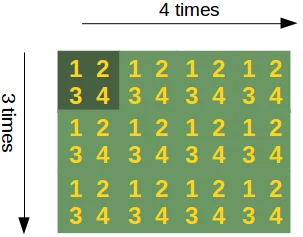
If this reminds you of tiling a bathroom or a kitchen, you are on the right track: The function which Numpy provides for this task is called "tile".
The formal syntax of tile looks like this:
tile(A, reps)
An array is constructed by repeating A the number of times given by reps.
'reps' is usually a tuple (or list) which defines the number of repetitions along the corresponding axis / directions. if we set reps to (3, 4) for example, A will be repeated 3 times for the "rows" and 4 times in the direction of the columna. We demonstrate this in the following example:
import numpy as np
x = np.array([ [1, 2], [3, 4]])
np.tile(x, (3,4))
OUTPUT:
array([[1, 2, 1, 2, 1, 2, 1, 2],
[3, 4, 3, 4, 3, 4, 3, 4],
[1, 2, 1, 2, 1, 2, 1, 2],
[3, 4, 3, 4, 3, 4, 3, 4],
[1, 2, 1, 2, 1, 2, 1, 2],
[3, 4, 3, 4, 3, 4, 3, 4]])
import numpy as np
x = np.array([ 3.4])
y = np.tile(x, (5,))
print(y)
OUTPUT:
[3.4 3.4 3.4 3.4 3.4]
In the previous tile example, we could have written y = np.tile(x, 5) as well.
If we stick to writing reps in the tuple or list form, or consider reps = 5 as an abbreviation for reps = (5,), the following is true:
If 'reps' has length n, the dimension of the resulting array will be the maximum of n and A.ndim.
If 'A.ndim < n, 'A' is promoted to be n-dimensional by prepending new axes. So a shape (5,) array is promoted to (1, 5) for 2-D replication, or shape (1, 1, 5) for 3-D replication. If this is not the desired behavior, promote 'A' to n-dimensions manually before calling this function.
If 'A.ndim > d', 'reps' is promoted to 'A'.ndim by pre-pending 1's to it.
Thus for an array 'A' of shape (2, 3, 4, 5), a 'reps' of (2, 2) is treated as (1, 1, 2, 2).
Further examples:
import numpy as np
x = np.array([[1, 2], [3, 4]])
print(np.tile(x, 2))
OUTPUT:
[[1 2 1 2] [3 4 3 4]]
import numpy as np
x = np.array([[1, 2], [3, 4]])
print(np.tile(x, (2, 1)))
OUTPUT:
[[1 2] [3 4] [1 2] [3 4]]
import numpy as np
x = np.array([[1, 2], [3, 4]])
print(np.tile(x, (2, 2)))
OUTPUT:
[[1 2 1 2] [3 4 3 4] [1 2 1 2] [3 4 3 4]]
Live Python training
Upcoming online Courses
23 Jun to 27 Jun 2025
28 Jul to 01 Aug 2025
08 Sep to 12 Sep 2025
20 Oct to 24 Oct 2025
04 Jun to 06 Jun 2025
30 Jul to 01 Aug 2025
10 Sep to 12 Sep 2025
22 Oct to 24 Oct 2025
Efficient Data Analysis with Pandas
02 Jun to 03 Jun 2025
23 Jun to 24 Jun 2025
28 Jul to 29 Jul 2025
08 Sep to 09 Sep 2025
20 Oct to 21 Oct 2025
04 Jun to 06 Jun 2025
10 Sep to 12 Sep 2025
22 Oct to 24 Oct 2025
See our Python training courses
