8. Finite State Machine in Python

By Bernd Klein. Last modified: 01 Feb 2022.

On this page ➤

A "Finite State Machine" (abbreviated FSM), also called "State Machine" or "Finite State Automaton" is an abstract machine which consists of a set of states (including the initial state and one or more end states), a set of input events, a set of output events, and a state transition function. A transition function takes the current state and an input event as an input and returns the new set of output events and the next (new) state. Some of the states are used as "terminal states". The operation of an FSM begins with a special state, called the start state, proceeds through transitions depending on input to different states and normally ends in terminal or end states. A state which marks a successful flow of operation is known as an accept state.

Leonardo Da Vinci Flying Machine

Mathematical Model

A deterministic finite state machine or acceptor deterministic finite state machine is a quintuple

(Σ,S,s₀,δ,F),

where:

Σ is the input alphabet (a finite, non-empty set of symbols).
S is a finite, non-empty set of states.
s₀ is an initial state, an element of S.
δ is the state-transition function: δ : S x Σ → S
(in a nondeterministic finite state machine it would be δ : S x Σ → ℘(S), i.e., δ would return a set of states). (℘(S) is the Power set of S)
F is the set of final states, a (possibly empty) subset of S.

Live Python training

Enjoying this page? We offer live Python training courses covering the content of this site.

See: Live Python courses overview

Enrol here

A Simple Example

We want to recognize the meaning of very small sentences with an extremely limited vocabulary and syntax.

These sentences should start with "Python is" followed by

an adjective or
the word "not" followed by an adjective. e.g.

"Python is great" → positive meaning

"Python is stupid" → negative meaning

"Python is not ugly" → positive meaning

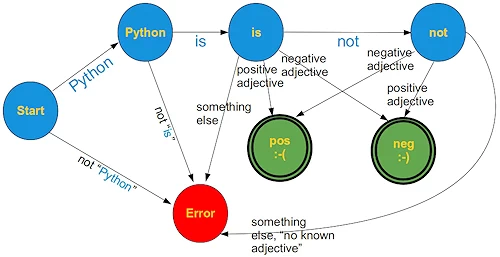
Finite state machine example

A Finite State Machine in Python

To implement the previous example, we program first a general Finite State Machine in Python.

class StateMachine:
    
    def __init__(self):
        self.handlers = {}
        self.startState = None
        self.endStates = []

    def add_state(self, name, handler, end_state=0):
        name = name.upper()
        self.handlers[name] = handler
        if end_state:
            self.endStates.append(name)

    def set_start(self, name):
        self.startState = name.upper()

    def run(self, cargo):
        try:
            handler = self.handlers[self.startState]
        except:
            raise InitializationError("must call .set_start() before .run()")
        if not self.endStates:
            raise  InitializationError("at least one state must be an end_state")
    
        while True:
            (newState, cargo) = handler(cargo)
            if newState.upper() in self.endStates:
                print("reached ", newState)
                break 
            else:
                handler = self.handlers[newState.upper()]

This general FSM is used in the next program:

positive_adjectives = ["great","super", "fun", "entertaining", "easy"]
negative_adjectives = ["boring", "difficult", "ugly", "bad"]

def start_transitions(txt):
    splitted_txt = txt.split(None,1)
    word, txt = splitted_txt if len(splitted_txt) > 1 else (txt,"")
    if word == "Python":
        newState = "Python_state"
    else:
        newState = "error_state"
    return (newState, txt)

def python_state_transitions(txt):
    splitted_txt = txt.split(None,1)
    word, txt = splitted_txt if len(splitted_txt) > 1 else (txt,"")
    if word == "is":
        newState = "is_state"
    else:
        newState = "error_state"
    return (newState, txt)

def is_state_transitions(txt):
    splitted_txt = txt.split(None,1)
    word, txt = splitted_txt if len(splitted_txt) > 1 else (txt,"")
    if word == "not":
        newState = "not_state"
    elif word in positive_adjectives:
        newState = "pos_state"
    elif word in negative_adjectives:
        newState = "neg_state"
    else:
        newState = "error_state"
    return (newState, txt)

def not_state_transitions(txt):
    splitted_txt = txt.split(None,1)
    word, txt = splitted_txt if len(splitted_txt) > 1 else (txt,"")
    if word in positive_adjectives:
        newState = "neg_state"
    elif word in negative_adjectives:
        newState = "pos_state"
    else:
        newState = "error_state"
    return (newState, txt)

def neg_state(txt):
    print("Hallo")
    return ("neg_state", "")


m = StateMachine()
m.add_state("Start", start_transitions)
m.add_state("Python_state", python_state_transitions)
m.add_state("is_state", is_state_transitions)
m.add_state("not_state", not_state_transitions)
m.add_state("neg_state", None, end_state=1)
m.add_state("pos_state", None, end_state=1)
m.add_state("error_state", None, end_state=1)
m.set_start("Start")
m.run("Python is great")
m.run("Python is difficult")
m.run("Perl is ugly")

OUTPUT:

reached  pos_state
reached  neg_state
reached  error_state

Live Python training

Enjoying this page? We offer live Python training courses covering the content of this site.

See: Live Python courses overview

Enrol here