Python Course

Advanced Topics

Text Processing and Python

What is text processing? Generally speaking it means taking some form of textual information and working on it, i.e. extracting, changing or adding information. Programmes and system administrators use text processing, when working with log files, configuration files, access files and so on.

Python is well suited for text processing.

---

This website is created by:



Python Training Courses in Toronto, Canada
On site trainings in Europe, Canada and the US.

---

---

We also like to thank Denise Mitchinson for providing the stylesheet of this website.

This topic in German / Deutsche Version: Einführung in die Text-Klassifikation

Python Courses

This example is taken from the Python course
"Python Text Processing Course" by Bodenseo.

Text Classification

Though the automated classification (categorization) of texts has been flourishing in the last decade or so, is a history, which dates back to about 1960. The incredible increase in online documents, which has been mostly due to the expanding internet, has renewed the interst in automated document classification and data mining. While text classification in the beginning was based mainly on heuristic methods, i.e. applying a set of rules based on expert knowledge, nowadays the focus has turned to fully automatic learning and even clustering methods.
from: Text Classification at Bernd Klein.

Text Categorization and Classification

Introduction

Document classification/categorization is a topic in information science, a science dealing with the collection, analysis, classification, categorization, manipulation, retrieval, storage and propagation of information.

This might sound very abstract, but there are lots of situations nowadays, where companies are in need of automatic classification or categorization of documents. Just think about a large company with thousands of incoming mail pieces per day, both eletronic or paper based. Lot's of these mail pieces are without specific addressee names or departments. Somebody has to read these texts and has to decide what kind of a letter it is ("change of address", "complaints letter", "inquiry about products", and so on) and to whom the document should be proceeded. This "somebody" can be an automated text classification system.


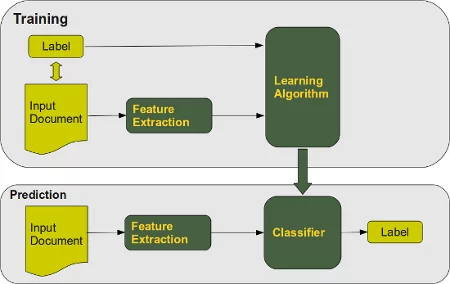
Automated text classification, also called categorization of texts, has a history, which dates back to the beginning of the 1960s. But the incredible increase in available online documents in the last two decades, due to the expanding internet, has intensified and renewed the interest in automated document classification and data mining. In the beginning text classification focussed on heuristic methods, i.e. solving the task by applying a set of rules based on expert knowledge. This approach proved to be highly inefficient, so nowadays the focus has turned to fully automatic learning and clustering methods.


The task of text classification consists in assigning a document to one or more categories, based on the semantic content of the document. Document classification tasks can be divided into three kinds:

• supervised document classification is performed by an external mechanism, usually human feedback, which provides the necessary information for the correct classification of documents,
• semi-supervised document classification, a mixture between supervised and unsupervised classification: some documents or parts of documents are labeled by external assistance,
• unsupervised document classification is entirely executed without reference to external information.

We will implement a text classifier in Python using Naive Bayes. Naive Bayes is the most commonly used text classifier and it is the focus of research in text classification. A Naive Bayes classifier is based on the application of Bayes' theorem with strong independence assumptions. "Strong independence" means: the presence or absence of a particular feature of a class is unrelated to the presence or absence of any other feature. Naive Bayes is well suited for multiclass text classification.

Formal Definition

Let C = { c₁, c₂, ... c_m} be a set of categories (classes) and D = { d₁, d₂, ... d_n} a set of documents.

The task of the text classification consists in assigning to each pair ( c_i, d_j ) of C x D (with 1 ≤ i ≤ m and 1 ≤ j ≤ n) a value of 0 or 1, i.e. the value 0, if the document d_j doesn't belong to c_i

This mapping is sometimes refered to as the decision matrix:

	d1	...	dj	...	dn
c1	a11	...	a1j	...	a1n
...	...	...	...	...	...
ci	ai1	...	aij	...	ain
...	...	...	...	...	...
cm	am1	...	amj	...	amn

The main approaches to solve this task are:

• Naive Bayes
• Support Vector Machine
• Nearest Neighbour

Conditional Probability

The Conditional probability P(A|B) is the probabilty of some event A, given the occurrence of some other event B. When in a random experiment the event B is known to have occurred, the possible outcomes of the experiment are reduced to B, and hence the probability of the occurrence of A is changed from the unconditional probability into the conditional probability given B. The Joint probabilty is the probability of two events in conjunction. That is, it is the probability of both events together. The joint probability of A and B is written as

P(A ∩ B), P(AB) or P(A,B)

The conditional probability is defined by

P(A|B) = P( A ∩ B) / P(B)

Example Conditional Probability

A medical research lab proposes a screening to test a large group of people for a disease. An argument against such screenings is the problem of false positive screening results.

Suppose 0,1% of the group suffer from the disease, and the rest is well:
P("sick") = 0,1 % = 0.01 and P("well") = 99,9 % = 0.999.

The following is true for a screening test:
If you have the disease, the test will be positive 99% of the time, and if you don't have it, the test will be negative 99% of the time: P("test positive" | "well") = 1 % and P("test negative" | "well") = 99 %.

Finally, suppose that when the test is applied to a person having the disease, there is a 1% chance of a false negative result (and 99% chance of getting a true positive result), i.e. P("test negative" | "sick") = 1 % and P("test positive" | "sick") = 99 %

	Sick	Healthy	Totals
Test result positive	99	999	1098
Test result negative	1	98901	98902
Totals	100	99900	100000

There are 999 False Positives and 1 False Negative.
Problem:
In many cases even medical professionals assume that "if you have this sickness, the test will be positive in 99 % of the time and if you don't have it, the test will be negative 99 % of the time. Out of the 1098 cases that report positive results only 99 (9 %) cases are correct and 999 cases are false positives (91 %), i.e. if a person gets a positive test result, the probabiltiy that he or she actually has the disease is just about 9 %. P("sick" | "test positive") = 99 / 1098 = 9.02 %

Naive Bayes Classifier

A Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem with strong (naïve) independence assumptions, i.e. an "independent feature model".
In other words: A naive Bayes classifier assumes that the presence (or absence) of a particular feature of a class is unrelated to the presence (or absence) of any other feature.

The Bayes Theorem:

P(A|B) = P(B|A)P(A) / P(B)

P(A|B) is the conditional probability of A, given B (posterior probability), P(B) is the prior probability of B and P(A) the prior probability of A. P(B|A) is the conditional probabilty of B given A, called the likelyhood.

An advantage of the naive Bayes classifier is that it requires only a small amount of training data to estimate the parameters necessary for classification.
Because independent variables are assumed, only the variances of the variables for each class need to be determined and not the entire covariance matrix.

Definition of independent events:
Two events E and F are independent, if both E and F have positive probability and if P(E|F) = P(E) and P(F|E) = P(F)

Formal Derivation of the Naive Bayes Classifier:

Let C = { c₁, c₂, ... c_m} be a set of classes or categories and D = { d₁, d₂, ... d_n} be a set of documents.
Each document is labeled with a class.
The set D of documents is used to train the classifier.
Classification consists in selecting the most probable class for an unknown document.

The number of times a word w_t occurs within a document d_i will be denoted as N_it. N_t^C denotes the number of times a word w_t ocurs in all documents of a given class C.
P(d_i|c_j) is 1, if d_i is labeled as c_j, 0 otherwise

The probability for a word wt given a class cj:


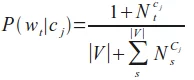
The probability for a class c_j is the quotient of the number of Documents of c_j and the number of documents of all classes, i.e. the learn set:



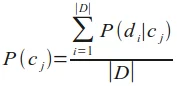
Finally, we come to the formula we need to classify an unknown document, i.e. the probability for a class c_j given a document d_i:


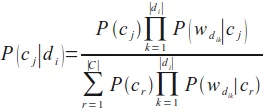
Unfortunately, the formula of P(c|d_i) we have just given is numerically not stable, because the denominator can be zero due to rounding errors. We change this by calculating the reciprocal and reformulate the expression as a sum of stable quotients:



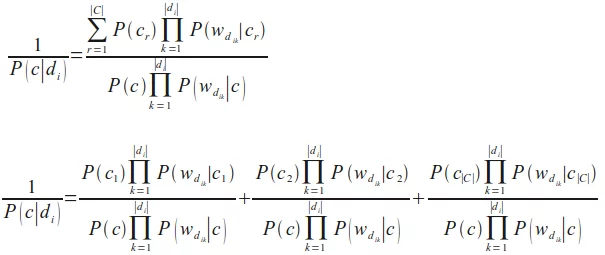
We can rewrite the previous formula into the following form, our final Naive Bayes classification formula, the one we will use in our Python implementation in the following chapter:

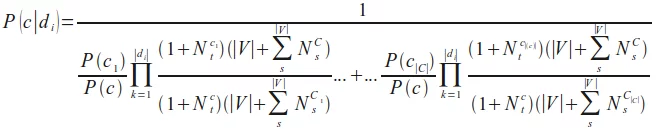
Further Reading

There are lots of articles on text classification. We just name a few, which we have used for our work:

• Fabrizio Sebastiani. A tutorial on automated text categorisation. In Analia Amandi and Alejandro Zunino (eds.), Proceedings of the 1st Argentinian Symposium on Artificial Intelligence (ASAI'99), Buenos Aires, AR, 1999, pp. 7-35.
• Lewis, David D., Naive (Bayes) at Forty: The independence assumption in informal retrieval, Lecture Notes in Computer Science (1998), 1398, Issue: 1398, Publisher: Springer, Pages: 4-15
• K. Nigam, A. McCallum, S. Thrun and T. Mitchell, Text classification from labeled and unlabeled documents using EM, Machine Learning 39 (2000) (2/3), pp. 103-134.