1. Recursive Functions
By Bernd Klein. Last modified: 01 Feb 2022.
Definition
Recursion has something to do with infinity. I know recursion has something to do with infinity. I think I know recursion has something to do with infinity. He is sure I think I know recursion has something to do with infinity. We doubt he is sure I think I know ...
We think that, you think, we convinced you now that, we can go on forever with this example of a recursion from natural language. Recursion is not only a fundamental feature of natural language, but of the human cognitive capacity. Our way of thinking is based on a recursive thinking processes. Even with a very simple grammar rule, like "An English sentence contains a subject and a predicate, and a predicate contains a verb, an object and a complement", we can demonstrate the infinite possibilities of the natural language.
The cognitive scientist and linguist Stephen Pinker phrases it like this: "With a few thousand nouns that can fill the subject slot and a few thousand verbs that can fill the predicate slot, one already has several million ways to open a sentence. The possible combinations quickly multiply out to unimaginably large numbers. Indeed, the repertoire of sentences is theoretically infinite, because the rules of language use a trick called recursion.
A recursive rule allows a phrase to contain an example of itself, as in She thinks that he thinks that they think that he knows and so on, ad infinitum. And if the number of sentences is infinite, the number of possible thoughts and intentions is infinite too, because virtually every sentence expresses a different thought or intention."1
We have to stop our short excursion to the use of recursion in natural language to come back to recursion in computer science and programs and finally to recursion in the programming language Python.
The adjective "recursive" originates from the Latin verb "recurrere", which means "to run back". And this is what a recursive definition or a recursive function does: It is "running back" or returning to itself. Most people who have done some mathematics, computer science or read a book about programming will have encountered the factorial, which is defined in mathematical terms as
n! = n * (n-1)!, if n > 1 and 0! = 1
It's used so often as an example for recursion because of its simplicity and clarity.
Live Python training
See our Python training courses
Definition of Recursion
Recursion is a method of programming or coding a problem, in which a function calls itself one or more times in its body. Usually, it is returning the return value of this function call. If a function definition satisfies the condition of recursion, we call this function a recursive function.
Termination condition: A recursive function has to fulfil an important condition to be used in a program: it has to terminate. A recursive function terminates, if with every recursive call the solution of the problem is downsized and moves towards a base case. A base case is a case, where the problem can be solved without further recursion. A recursion can end up in an infinite loop, if the base case is not met in the calls.
Example:
4! = 4 * 3! 3! = 3 * 2! 2! = 2 * 1
Replacing the calculated values gives us the following expression
4! = 4 * 3 * 2 * 1
In other words, recursion in computer science is a method where the solution to a problem is based on solving smaller instances of the same problem.
Recursive Functions in Python
Now we come to implement the factorial in Python. It's as easy and elegant as the mathematical definition.
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)
We can track how the function works by adding two print() functions to the previous function definition:
def factorial(n):
print("factorial has been called with n = " + str(n))
if n == 1:
return 1
else:
res = n * factorial(n-1)
print("intermediate result for ", n, " * factorial(" ,n-1, "): ",res)
return res
print(factorial(5))
OUTPUT:
factorial has been called with n = 5 factorial has been called with n = 4 factorial has been called with n = 3 factorial has been called with n = 2 factorial has been called with n = 1 intermediate result for 2 * factorial( 1 ): 2 intermediate result for 3 * factorial( 2 ): 6 intermediate result for 4 * factorial( 3 ): 24 intermediate result for 5 * factorial( 4 ): 120 120
Let's have a look at an iterative version of the factorial function.
def iterative_factorial(n):
result = 1
for i in range(2,n+1):
result *= i
return result
for i in range(5):
print(i, iterative_factorial(i))
OUTPUT:
0 1 1 1 2 2 3 6 4 24
It is common practice to extend the factorial function for 0 as an argument. It makes sense to define 0! to be 1, because there is exactly one permutation of zero objects, i.e. if nothing is to permute, "everything" is left in place. Another reason is that the number of ways to choose n elements among a set of n is calculated as n! divided by the product of n! and 0!.
All we have to do to implement this is to change the condition of the if statement:
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)
Fibonacci Numbers
Our treatise of recursion leads us now to another interesting case of recursion.
What do have sunflowers, the Golden ratio, fir tree cones, The Da Vinci Code, the song "Lateralus" by Tool, and the graphic on the right side in common? Right, the Fibonacci numbers. We are not introducing the Fibonacci numbers, because they are another useful example for recusive function. Trying to write a recursive function for this sequence of numbers, might lead to an inefficient program. In fact, so inefficient that it will not be useful. We introduce the Fibonacci numbers to show you the pitfalls of recursion.
The Fibonacci numbers are the numbers of the following sequence of integer values:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
The Fibonacci numbers are defined by:
$F_n = F_{n-} + F_{n-2}$
with $F_0 = 0$ and $F_1 = 1$
The Fibonacci sequence is named after the mathematician Leonardo of Pisa, who is better known as Fibonacci. In his book "Liber Abaci" (published in 1202) he introduced the sequence as an exercise dealing with bunnies. His sequence of the Fibonacci numbers begins with F1 = 1, while in modern mathematics the sequence starts with F0 = 0. But this has no effect on the other members of the sequence.
The Fibonacci numbers are the result of an artificial rabbit population, satisfying the following conditions:
- a newly born pair of rabbits, one male, one female, build the initial population
- these rabbits are able to mate at the age of one month so that at the end of its second month a female can bring forth another pair of rabbits
- these rabbits are immortal
- a mating pair always produces one new pair (one male, one female) every month from the second month onwards
The Fibonacci numbers are the numbers of rabbit pairs after n months, i.e. after 10 months we will have $F_10$ rabits.
The Fibonacci numbers are easy to write as a Python function. It's more or less a one to one mapping from the mathematical definition:
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
An iterative solution is also easy to write, though the recursive solution looks more like the definition:
def fibi(n):
old, new = 0, 1
if n == 0:
return 0
for i in range(n-1):
old, new = new, old + new
return new
We will write a module with the name fibonacci containing both the funciton fib and fibi. To do this you have to copy the following code into a file with the name fibonacci0.py:
""" A module containing both a recursive and an iterative implementation of the Fibonacci function.
The purpose of this module consists in showing the inefficiency of a purely recursive implementation of Fibonacci! """
def fib(n):
""" recursive version of the Fibonacci function """
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
def fibi(n):
""" iterative version of the Fibonacci function """
old, new = 0, 1
if n == 0:
return 0
for i in range(n-1):
old, new = new, old + new
return new
OUTPUT:
Overwriting fibonacci0.py
If you check the functions fib() and fibi(), you will find out that the iterative version fibi() is a lot faster than the recursive version fib(). To get an idea of how much this "a lot faster" can be, we have written a script, which uses the timeit module, to measure the calls. To do this, we save the function definitions for fib and fibi in a file fibonacci.py, which we can import in the program (fibonacci_runit.py) below:
from timeit import Timer
t1 = Timer("fib(10)","from fibonacci import fib")
for i in range(1, 20):
cmd = "fib(" + str(i) + ")"
t1 = Timer(cmd, "from fibonacci import fib")
time1 = t1.timeit(3)
cmd = "fibi(" + str(i) + ")"
t2 = Timer(cmd, "from fibonacci import fibi")
time2 = t2.timeit(3)
print(f"n={i:2d}, fib: {time1:8.6f}, fibi: {time2:7.6f}, time1/time2: {time1/time2:10.2f}")
OUTPUT:
n= 1, fib: 0.000001, fibi: 0.000002, time1/time2: 0.50 n= 2, fib: 0.000002, fibi: 0.000002, time1/time2: 0.85 n= 3, fib: 0.000003, fibi: 0.000002, time1/time2: 1.11 n= 4, fib: 0.000004, fibi: 0.000003, time1/time2: 1.45 n= 5, fib: 0.000011, fibi: 0.000003, time1/time2: 3.35 n= 6, fib: 0.000008, fibi: 0.000003, time1/time2: 2.98 n= 7, fib: 0.000012, fibi: 0.000002, time1/time2: 5.05 n= 8, fib: 0.000018, fibi: 0.000002, time1/time2: 7.98 n= 9, fib: 0.000029, fibi: 0.000002, time1/time2: 12.15 n=10, fib: 0.000046, fibi: 0.000003, time1/time2: 18.18 n=11, fib: 0.000075, fibi: 0.000003, time1/time2: 28.42 n=12, fib: 0.000153, fibi: 0.000003, time1/time2: 51.99 n=13, fib: 0.000194, fibi: 0.000003, time1/time2: 72.11 n=14, fib: 0.000323, fibi: 0.000003, time1/time2: 109.50 n=15, fib: 0.001015, fibi: 0.000008, time1/time2: 134.65 n=16, fib: 0.002165, fibi: 0.000008, time1/time2: 261.11 n=17, fib: 0.003795, fibi: 0.000019, time1/time2: 198.87 n=18, fib: 0.006021, fibi: 0.000010, time1/time2: 574.59 n=19, fib: 0.008807, fibi: 0.000011, time1/time2: 785.54
time1 is the time in seconds it takes for 3 calls to fib(n) and time2 respectively the time for fibi(n).
What's wrong with our recursive implementation?
Let's have a look at the calculation tree, i.e. the order in which the functions are called. fib() is substituted by f().
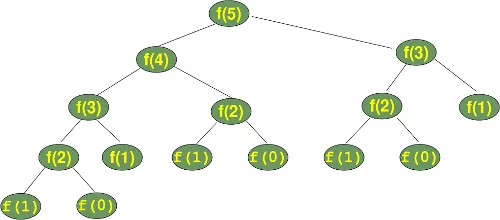
We can see that the subtree f(2) appears 3 times and the subtree for the calculation of f(3) two times. If you imagine extending this tree for f(6), you will understand that f(4) will be called two times, f(3) three times and so on. This means, our recursion doesn't remember previously calculated values.
We can implement a "memory" for our recursive version by using a dictionary to save the previously calculated values. We call this version fibm:
memo = {0:0, 1:1}
def fibm(n):
if not n in memo:
memo[n] = fibm(n-1) + fibm(n-2)
return memo[n]
Before we can do some timing on the new version, we add it to our fibonacci module:
""" A module containing both a recursive and an iterative implementation of the Fibonacci function.
The purpose of this module consists in showing the inefficiency of a purely recursive implementation of Fibonacci! """
def fib(n):
""" recursive version of the Fibonacci function """
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
def fibi(n):
""" iterative version of the Fibonacci function """
old, new = 0, 1
if n == 0:
return 0
for i in range(n-1):
old, new = new, old + new
return new
memo = {0:0, 1:1}
def fibm(n):
""" recursive Fibonacci function which memoizes previously
calculated values with the help of a dictionary memo"""
if not n in memo:
memo[n] = fibm(n-1) + fibm(n-2)
return memo[n]
OUTPUT:
Overwriting fibonacci.py
We time it again to compare it with fibi():
from timeit import Timer
from fibonacci import fib
t1 = Timer("fib(10)","from fibonacci import fib")
for i in range(1, 20):
s = "fibm(" + str(i) + ")"
t1 = Timer(s,"from fibonacci import fibm")
time1 = t1.timeit(3)
s = "fibi(" + str(i) + ")"
t2 = Timer(s,"from fibonacci import fibi")
time2 = t2.timeit(3)
print(f"n={i:2d}, fibm: {time1:8.6f}, fibi: {time2:7.6f}, time1/time2: {time1/time2:10.2f}")
OUTPUT:
n= 1, fibm: 0.000002, fibi: 0.000002, time1/time2: 0.68 n= 2, fibm: 0.000001, fibi: 0.000002, time1/time2: 0.63 n= 3, fibm: 0.000001, fibi: 0.000002, time1/time2: 0.51 n= 4, fibm: 0.000001, fibi: 0.000002, time1/time2: 0.46 n= 5, fibm: 0.000001, fibi: 0.000002, time1/time2: 0.48 n= 6, fibm: 0.000001, fibi: 0.000002, time1/time2: 0.41 n= 7, fibm: 0.000001, fibi: 0.000002, time1/time2: 0.41 n= 8, fibm: 0.000001, fibi: 0.000011, time1/time2: 0.10 n= 9, fibm: 0.000001, fibi: 0.000002, time1/time2: 0.40 n=10, fibm: 0.000001, fibi: 0.000002, time1/time2: 0.36 n=11, fibm: 0.000001, fibi: 0.000003, time1/time2: 0.38 n=12, fibm: 0.000001, fibi: 0.000003, time1/time2: 0.35 n=13, fibm: 0.000001, fibi: 0.000003, time1/time2: 0.44 n=14, fibm: 0.000001, fibi: 0.000003, time1/time2: 0.36 n=15, fibm: 0.000001, fibi: 0.000003, time1/time2: 0.35 n=16, fibm: 0.000001, fibi: 0.000004, time1/time2: 0.34 n=17, fibm: 0.000001, fibi: 0.000003, time1/time2: 0.33 n=18, fibm: 0.000001, fibi: 0.000004, time1/time2: 0.29 n=19, fibm: 0.000001, fibi: 0.000004, time1/time2: 0.27
We can see that it is even faster than the iterative version. Of course, the larger the arguments, the greater the benefit of our memorization:
We can also define a recursive algorithm for our Fibonacci function by using a class with callabe instances, i.e. by using the special method call. This way, we will be able to hide the dictionary in an elegant way. We used a general approach which allows as to define also functions similar to Fibonacci, like the Lucas function. This means that we can create Fibonacci-like number sequences by instantiating instances of this class. Basically, the building principle, i.e. the sum of the previous two numbers, will be the same. They will differ by the two initial values:
class FibonacciLike:
def __init__(self, i1=0, i2=1):
self.memo = {0:i1, 1:i2}
def __call__(self, n):
if n not in self.memo:
self.memo[n] = self.__call__(n-1) + self.__call__(n-2)
return self.memo[n]
# We create a callable to create the Fibonacci numbers:
fib = FibonacciLike()
# This will create a callable to create the Lucas number series:
lucas = FibonacciLike(2, 1)
for i in range(1, 16):
print(i, fib(i), lucas(i))
OUTPUT:
1 1 1 2 1 3 3 2 4 4 3 7 5 5 11 6 8 18 7 13 29 8 21 47 9 34 76 10 55 123 11 89 199 12 144 322 13 233 521 14 377 843 15 610 1364
The Lucas numbers or Lucas series are an integer sequence named after the mathematician François Édouard Anatole Lucas (1842–91), who studied both that sequence and the closely related Fibonacci numbers. The Lucas numbers have the same creation rule as the Fibonacci number, i.e. the sum of the two previous numbers, but the values for 0 and 1 are different.
Generalized Fibonacci Sequence
We will demonstrate now that our approach is also suitable to calculate arbitrary generalized Fibonacci sequences. The Fibonacci sequence depends on the two preceding values. We generalize this concept now by defining a k-Fib sequence in the following way
Given a fixed natural number k and k >= 2. Also given k initial values $i_0, i_1, \ldots i_{k-1}$
satisfying $F_k(0) = i_0, \ldots F_k(k-1) = i_{k-1}$
The function also needs $k$ cofficients $c_0, c_1, \ldots c_{k-1}$
$F_k(n)$ is defined as
$$F_k(n) = a_0 \cdot F_k(n-1) + a_1 \cdot F_k(n-2) \ldots a_{k-1} \cdot F_k(n-k)$$
with $k <= n$
class kFibonacci:
def __init__(self, k, initials, coefficients):
self.memo = dict(zip(range(k), initials))
self.coeffs = coefficients
self.k = k
def __call__(self, n):
k = self.k
if n not in self.memo:
result = 0
for coeff, i in zip(self.coeffs, range(1, k+1)):
result += coeff * self.__call__(n-i)
self.memo[n] = result
return self.memo[n]
fib = kFibonacci(2, (0, 1), (1, 1))
lucas = kFibonacci(2, (2, 1), (1, 1))
for i in range(1, 16):
print(i, fib(i), lucas(i))
OUTPUT:
1 1 1 2 1 3 3 2 4 4 3 7 5 5 11 6 8 18 7 13 29 8 21 47 9 34 76 10 55 123 11 89 199 12 144 322 13 233 521 14 377 843 15 610 1364
The sequence of Pell numbers start with 1, 2, 5, 12, 29, ...
The function is
$P(n) = 2 \cdot P(n-1) + P(n-2)$ with $P(0) = 1$ and $P(1) = 1$
It is easy to formulate this sequence with our kFibonacci class:
P = kFibonacci(2, (1, 2), (2, 1))
for i in range(10):
print(i, P(i))
OUTPUT:
0 1 1 2 2 5 3 12 4 29 5 70 6 169 7 408 8 985 9 2378
We can create another interesting series by adding the sum of previous two Pell numbers between two Pell numbers P(i) and P(i+1). We get:
$P(0), P(1), P(0)+P(1), P(2), P(1)+P(2), P(3), P(2)+P(3), \ldots$
corresponding to: $1, 2, 3, 5, 7, 12, 17, 29, \ldots $
def nP(n):
if n < 2:
return P(n)
else:
i = n // 2 + 1
if n % 2: # n is odd
return P(i)
else:
return P(i-1) + P(i-2)
for i in range(20):
print(nP(i), end=", ")
OUTPUT:
1, 2, 3, 5, 7, 12, 17, 29, 41, 70, 99, 169, 239, 408, 577, 985, 1393, 2378, 3363, 5741,
If you have a close look at the numbers, you can see that there is another rule in this sequence. We can define nP as
$nP(n) = 2 \cdot nP(n-2) + nP(n-4)$ with $n > 3$ and the start values $1, 2, 3, 5$
This is another easy application for our kFibonacci class:
nP = kFibonacci(4, (1, 2, 3, 5), (0, 2, 0, 1))
for i in range(20):
print(nP(i), end=", ")
OUTPUT:
1, 2, 3, 5, 7, 12, 17, 29, 41, 70, 99, 169, 239, 408, 577, 985, 1393, 2378, 3363, 5741,
An interesting mathematical fact: For every odd n the quotient of $P(n)$ by $P(n-1)$ is an approximation of $\sqrt{2}$. If n is even, the quotient is an approximation of $1 + {1 \over {\sqrt{2}}}$
sqrt2 = 2 ** 0.5
print("Square root of 2: ", sqrt2)
print("Square root of 3: ", 1 + 1 / sqrt2)
for i in range(1, 20):
print(nP(i) / nP(i-1), end=", ")
OUTPUT:
Square root of 2: 1.4142135623730951 Square root of 3: 1.7071067811865475 2.0, 1.5, 1.6666666666666667, 1.4, 1.7142857142857142, 1.4166666666666667, 1.7058823529411764, 1.4137931034482758, 1.7073170731707317, 1.4142857142857144, 1.707070707070707, 1.4142011834319526, 1.707112970711297, 1.4142156862745099, 1.707105719237435, 1.4142131979695431, 1.7071069633883704, 1.4142136248948696, 1.7071067499256616,
Live Python training
See our Python training courses
More about Recursion in Python

If you want to learn more on recursion, we suggest that you try to solve the following exercises. Please do not peer at the solutions, before you have given your best. If you have thought about a task for a while and you are still not capable of solving the exercise, you may consult our sample solutions.
In our section "Advanced Topics" of our tutorial we have a comprehensive treatment of the game or puzzle "Towers of Hanoi". Of course, we solve it with a function using a recursive function. The "Hanoi problem" is special, because a recursive solution almost forces itself on the programmer, while the iterative solution of the game is hard to find and to grasp.
Exercises
Exercise 1
Think of a recursive version of the function f(n) = 3 * n, i.e. the multiples of 3
Exercise 2
Write a recursive Python function that returns the sum of the first n integers. (Hint: The function will be similiar to the factorial function!)
Exercise 3
Write a function which implements the Pascal's triangle:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Exercise 4
The Fibonacci numbers are hidden inside of Pascal's triangle. If you sum up the coloured numbers of the following triangle, you will get the 7th Fibonacci number:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
Write a recursive program to calculate the Fibonacci numbers, using Pascal's triangle.
Exercise 5
Implement a recursive function in Python for the sieve of Eratosthenes.
The sieve of Eratosthenes is a simple algorithm for finding all prime numbers up to a specified integer. It was created by the ancient Greek mathematician Eratosthenes. The algorithm to find all the prime numbers less than or equal to a given integer n:
- Create a list of integers from two to n: 2, 3, 4, ..., n
- Start with a counter i set to 2, i.e. the first prime number
- Starting from i+i, count up by i and remove those numbers from the list, i.e. 2i, 3i, 4*i, etc..
- Find the first number of the list following i. This is the next prime number.
- Set i to the number found in the previous step
- Repeat steps 3 and 4 until i is greater than n. (As an improvement: It's enough to go to the square root of n)
- All the numbers, which are still in the list, are prime numbers
You can easily see that we would be inefficient, if we strictly used this algorithm, e.g. we will try to remove the multiples of 4, although they have been already removed by the multiples of 2. So it's enough to produce the multiples of all the prime numbers up to the square root of n. We can recursively create these sets.
Exercise 6
Write a recursive function fib_indexfib(), which returns the index of a number in the Fibonacci sequence, if the number is an element of this sequence, and returns -1 if the number is not contained in it, i.e.
$fib(fib\_index(n)) == n$
Exercise 7
The sum of the squares of two consecutive Fibonacci numbers is also a Fibonacci number, e.g. 2 and 3 are elements of the Fibonacci sequence and 22 + 33 = 13 corresponds to Fib(7).Use the previous function to find the position of the sum of the squares of two consecutive numbers in the Fibonacci sequence.
Mathematical explanation: Let a and b be two successive Fibonacci numbers with a prior to b. The Fibonacci sequence starting with the number "a" looks like this:
0 a
1 b
2 a + b
3 a + 2b
4 2a + 3b
5 3a + 5b
6 5a + 8b
We can see that the Fibonacci numbers appear as factors for a and b. The n-th element in this sequence can be calculated with the following formula:
$F(n) = Fib(n-1) \cdot a + Fib(n) \cdot b$
From this we can conclude that for a natural number n, n>1, the following holds true:
$Fib(2 \cdot n + 1) = Fib(n)^2 + Fib(n+1)^2$
Exercise 8
The tribonacci numbers are like the Fibonacci numbers, but instead of starting with two predetermined terms, the sequence starts with three predetermined terms and each term afterwards is the sum of the preceding three terms. The first few tribonacci numbers are:
0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, ...
The tetranacci numbers start with four predetermined terms, each term afterwards being the sum of the preceding four terms. The first few tetranacci numbers are:
0, 0, 0, 1, 1, 2, 4, 8, 15, 29, 56, 108, 208, 401, 773, 1490, 2872, 5536, 10671, 20569, 39648, ...
This continues in the same way for pentanacci, hexanacci, heptanacci, octanacci, and so on.
Write a function for the tribonacci and tetranacci numbers.
Exercise 9:
What if somebody wants to check the parameters in a recursive function? For example the factorial function. Okay, please write a recursive version of factorial, which checks the parameters. Maybe you did it in a perfect way, but maybe not. Can you improve your version? Get rid of unnecessary tests?
Live Python training
See our Python training courses
Solutions
Solution to Exercise 1
Mathematically, we can write it like this:
$f(1) = 3, $
$f(n+1) = f(n) + 3$
A Python function can be written like this:
def mult3(n):
if n == 1:
return 3
else:
return mult3(n-1) + 3
for i in range(1,10):
print(mult3(i))
OUTPUT:
3 6 9 12 15 18 21 24 27
Solution to Exercise 2
def sum_n(n):
if n== 0:
return 0
else:
return n + sum_n(n-1)
Solution to Exercise 3: Generating the Pascal triangle:
def pascal(n):
if n == 1:
return [1]
else:
line = [1]
previous_line = pascal(n-1)
for i in range(len(previous_line)-1):
line.append(previous_line[i] + previous_line[i+1])
line += [1]
return line
print(pascal(6))
OUTPUT:
[1, 5, 10, 10, 5, 1]
Alternatively, we can write a function using list comprehension:
def pascal(n):
if n == 1:
return [1]
else:
p_line = pascal(n-1)
line = [ p_line[i]+p_line[i+1] for i in range(len(p_line)-1)]
line.insert(0,1)
line.append(1)
return line
print(pascal(6))
OUTPUT:
[1, 5, 10, 10, 5, 1]
Solution to Exercise 4
Producing the Fibonacci numbers out of Pascal's triangle:
def fib_pascal(n,fib_pos):
if n == 1:
line = [1]
fib_sum = 1 if fib_pos == 0 else 0
else:
line = [1]
(previous_line, fib_sum) = fib_pascal(n-1, fib_pos+1)
for i in range(len(previous_line)-1):
line.append(previous_line[i] + previous_line[i+1])
line += [1]
if fib_pos < len(line):
fib_sum += line[fib_pos]
return (line, fib_sum)
def fib(n):
return fib_pascal(n,0)[1]
# and now printing out the first ten Fibonacci numbers:
for i in range(1,10):
print(fib(i))
OUTPUT:
1 1 2 3 5 8 13 21 34
Solution to Exercise 5
The following program implements the sieve of Eratosthenes according to the rules of the task in an iterative way. It will print out the first 100 prime numbers.
from math import sqrt
def sieve(n):
# returns all primes between 2 and n
primes = list(range(2,n+1))
max = sqrt(n)
num = 2
while num < max:
i = num
while i <= n:
i += num
if i in primes:
primes.remove(i)
for j in primes:
if j > num:
num = j
break
return primes
print(sieve(100))
OUTPUT:
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
But this chapter of our tutorial is about recursion and recursive functions, and we have demanded a recursive function to calculate the prime numbers. To understand the following solution, you may confer our chapter about List Comprehension:
from math import sqrt
def primes(n):
if n == 0:
return []
elif n == 1:
return []
else:
p = primes(int(sqrt(n)))
no_p = [j for i in p for j in range(i*2, n + 1, i)]
p = [x for x in range(2, n + 1) if x not in no_p]
return p
print(primes(100))
OUTPUT:
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
Solution to Exercise 6
memo = {0:0, 1:1}
def fib(n):
if not n in memo:
memo[n] = fib(n-1) + fib(n-2)
return memo[n]
def fib_index(*x):
""" finds the natural number i with fib(i) == n """
if len(x) == 1:
# started by user
# find index starting from 0
return fib_index(x[0], 0)
else:
n = fib(x[1])
m = x[0]
if n > m:
return -1
elif n == m:
return x[1]
else:
return fib_index(m, x[1]+1)
# code from the previous example with the functions fib() and find_index()
print(" index of a | a | b | sum of squares | index ")
print("=====================================================")
for i in range(15):
square = fib(i)**2 + fib(i+1)**2
print(f"{i:12d}|{fib(i):6d}|{fib(i+1):9d}|{square:14d}|{fib_index(square):5d}")
OUTPUT:
index of a | a | b | sum of squares | index
=====================================================
0| 0| 1| 1| 1
1| 1| 1| 2| 3
2| 1| 2| 5| 5
3| 2| 3| 13| 7
4| 3| 5| 34| 9
5| 5| 8| 89| 11
6| 8| 13| 233| 13
7| 13| 21| 610| 15
8| 21| 34| 1597| 17
9| 34| 55| 4181| 19
10| 55| 89| 10946| 21
11| 89| 144| 28657| 23
12| 144| 233| 75025| 25
13| 233| 377| 196418| 27
14| 377| 610| 514229| 29
Solution to Exercise 8
We will use the class kFibonacci which we have defined in this chapter.
tribonacci = kFibonacci(3, (0, 0, 1), (1, 1, 1))
for i in range(20):
print(tribonacci(i), end=", ")
OUTPUT:
0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513,
tetranacci = kFibonacci(4, (0, 0, 0, 1), (1, 1, 1, 1))
for i in range(20):
print(tetranacci(i), end=", ")
OUTPUT:
0, 0, 0, 1, 1, 2, 4, 8, 15, 29, 56, 108, 208, 401, 773, 1490, 2872, 5536, 10671, 20569,
We can easily create them like this:
prefixes = ['tribo', 'tetra', 'pentra', 'hexa', 'hepta', 'octa']
for k, prefix in zip(range(len(prefixes)), prefixes):
cmd = prefix + "nacci = kFibonacci("
cmd += str(k+3) + ", (" + "0, " * (k+2) + "1), "
cmd += "(" + "1, " * (k+2) + "1))"
print(cmd)
exec(cmd)
print("\nTesting the octanacci function: ")
for i in range(20):
print(octanacci(i), end=", ")
OUTPUT:
tribonacci = kFibonacci(3, (0, 0, 1), (1, 1, 1)) tetranacci = kFibonacci(4, (0, 0, 0, 1), (1, 1, 1, 1)) pentranacci = kFibonacci(5, (0, 0, 0, 0, 1), (1, 1, 1, 1, 1)) hexanacci = kFibonacci(6, (0, 0, 0, 0, 0, 1), (1, 1, 1, 1, 1, 1)) heptanacci = kFibonacci(7, (0, 0, 0, 0, 0, 0, 1), (1, 1, 1, 1, 1, 1, 1)) octanacci = kFibonacci(8, (0, 0, 0, 0, 0, 0, 0, 1), (1, 1, 1, 1, 1, 1, 1, 1)) Testing the octanacci function: 0, 0, 0, 0, 0, 0, 0, 1, 1, 2, 4, 8, 16, 32, 64, 128, 255, 509, 1016, 2028,
Solution to Exercise 9
def factorial(n):
""" calculates the factorial of n,
n should be an integer and n <= 0 """
if type(n) == int and n >=0:
if n == 0:
return 1
else:
return n * factorial(n-1)
else:
raise TypeError("n has to be a positive integer or zero")
What do you think about this solution? You call factorial(10) for example. The funciton will check, if 10 is a positive integer. The function will recursively call factorial(9). In this call the function will check again, if 9 is an integer. What else can it be? The first call had already checked 10 and all we did was subtracting 1 from 10.
We can overcome this problem by defining an inner function:
def factorial(n):
""" calculates the factorial of n,
n should be an integer and n <= 0 """
def inner_factorial(n):
if n == 0:
return 1
else:
return n * inner_factorial(n-1)
if type(n) == int and n >=0:
return inner_factorial(n)
else:
raise TypeError("n should be a positve int or 0")
print(factorial(10))
OUTPUT:
3628800
The test will only be performed on the first call with 10!
*Stephen Pinker, The Blank Slate, 2002
