1. Introduction to NumPy
By Bernd Klein. Last modified: 01 Feb 2022.
Introduction
NumPy is a module for Python. The name is an acronym for "Numeric Python" or "Numerical Python". It is pronounced /ˈnʌmpaɪ/ (NUM-py) or less often /ˈnʌmpi (NUM-pee)). It is an extension module for Python, mostly written in C. This makes sure that the precompiled mathematical and numerical functions and functionalities of Numpy guarantee great execution speed.
Furthermore, NumPy enriches the programming language Python with powerful data structures, implementing multi-dimensional arrays and matrices. These data structures guarantee efficient calculations with matrices and arrays. The implementation is even aiming at huge matrices and arrays, better know under the heading of "big data". Besides that the module supplies a large library of high-level mathematical functions to operate on these matrices and arrays.
SciPy (Scientific Python) is often mentioned in the same breath with NumPy. SciPy needs Numpy, as it is based on the data structures of Numpy and furthermore its basic creation and manipulation functions. It extends the capabilities of NumPy with further useful functions for minimization, regression, Fourier-transformation and many others.
Both NumPy and SciPy are not part of a basic Python installation. They have to be installed after the Python installation. NumPy has to be installed before installing SciPy.
The image above is the graphical visualisation of a matrix with 14 rows and 20 columns. It's a so-called Hinton diagram. The size of a square within this diagram corresponds to the size of the value of the depicted matrix. The colour determines, if the value is positive or negative. In our example: the colour red denotes negative values and the colour green denotes positive values.
NumPy is based on two earlier Python modules dealing with arrays. One of these is Numeric. Numeric is like NumPy a Python module for high-performance, numeric computing, but it is obsolete nowadays. Another predecessor of NumPy is Numarray, which is a complete rewrite of Numeric but is deprecated as well. NumPy is a merger of those two, i.e. it is build on the code of Numeric and the features of Numarray.
Live Python training
Enjoying this page? We offer live Python training courses covering the content of this site.
Comparison between Core Python and Numpy
When we say "Core Python", we mean Python without any special modules, i.e. especially without NumPy.
The advantages of Core Python:
- high-level number objects: integers, floating point
- containers: lists with cheap insertion and append methods, dictionaries with fast lookup
Advantages of using Numpy with Python:
- array oriented computing
- efficiently implemented multi-dimensional arrays
- designed for scientific computation
A Simple Numpy Example
Before we can use NumPy we will have to import it. It has to be imported like any other module:
import numpy
But you will hardly ever see this. Numpy is usually renamed to np:
import numpy as np
Our first simple Numpy example deals with temperatures. Given is a list with values, e.g. temperatures in Celsius:
cvalues = [20.1, 20.8, 21.9, 22.5, 22.7, 22.3, 21.8, 21.2, 20.9, 20.1]
We will turn our list "cvalues" into a one-dimensional numpy array:
C = np.array(cvalues)
print(C)
OUTPUT:
[20.1 20.8 21.9 22.5 22.7 22.3 21.8 21.2 20.9 20.1]
Let's assume, we want to turn the values into degrees Fahrenheit. This is very easy to accomplish with a numpy array. The solution to our problem can be achieved by simple scalar multiplication:
print(C * 9 / 5 + 32)
OUTPUT:
[68.18 69.44 71.42 72.5 72.86 72.14 71.24 70.16 69.62 68.18]
The array C has not been changed by this expression:
print(C)
OUTPUT:
[20.1 20.8 21.9 22.5 22.7 22.3 21.8 21.2 20.9 20.1]
Compared to this, the solution for our Python list looks awkward:
fvalues = [ x*9/5 + 32 for x in cvalues]
print(fvalues)
OUTPUT:
[68.18, 69.44, 71.42, 72.5, 72.86, 72.14, 71.24000000000001, 70.16, 69.62, 68.18]
So far, we referred to C as an array. The internal type is "ndarray" or to be even more precise "C is an instance of the class numpy.ndarray":
type(C)
OUTPUT:
numpy.ndarray
In the following, we will use the terms "array" and "ndarray" in most cases synonymously.
Live Python training
Enjoying this page? We offer live Python training courses covering the content of this site.
Upcoming online Courses
Graphical Representation of the Values
Even though we want to cover the module matplotlib not until a later chapter, we want to demonstrate how we can use this module to depict our temperature values. To do this, we us the package pyplot from matplotlib.
If you use the jupyter notebook, you might be well advised to include the following line of code to prevent an external window to pop up and to have your diagram included in the notebook:
%matplotlib inline
The code to generate a plot for our values looks like this:
import matplotlib.pyplot as plt
plt.plot(C)
plt.show()
The function plot uses the values of the array C for the values of the ordinate, i.e. the y-axis. The indices of the array C are taken as values for the abscissa, i.e. the x-axis.
Memory Consumption: ndarray and list
The main benefits of using numpy arrays should be smaller memory consumption and better runtime behaviour. We want to look at the memory usage of numpy arrays in this subchapter of our turorial and compare it to the memory consumption of Python lists.
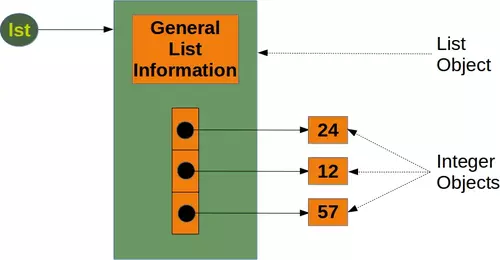
To calculate the memory consumption of the list from the above picture, we will use the function getsizeof from the module sys.
from sys import getsizeof as size
lst = [24, 12, 57]
size_of_list_object = size(lst) # only green box
size_of_elements = len(lst) * size(lst[0]) # 24, 12, 57
total_list_size = size_of_list_object + size_of_elements
print("Size without the size of the elements: ", size_of_list_object)
print("Size of all the elements: ", size_of_elements)
print("Total size of list, including elements: ", total_list_size)
OUTPUT:
Size without the size of the elements: 96 Size of all the elements: 84 Total size of list, including elements: 180
The size of a Python list consists of the general list information, the size needed for the references to the elements and the size of all the elements of the list. If we apply sys.getsizeof to a list, we get only the size without the size of the elements. In the previous example, we made the assumption that all the integer elements of our list have the same size. Of course, this is not valid in general, because memory consumption will be higher for larger integers.
We will check now, how the memory usage changes, if we add another integer element to the list. We also look at an empty list:
lst = [24, 12, 57, 42]
size_of_list_object = size(lst) # only green box
size_of_elements = len(lst) * size(lst[0]) # 24, 12, 57, 42
total_list_size = size_of_list_object + size_of_elements
print("Size without the size of the elements: ", size_of_list_object)
print("Size of all the elements: ", size_of_elements)
print("Total size of list, including elements: ", total_list_size)
lst = []
print("Emtpy list size: ", size(lst))
OUTPUT:
Size without the size of the elements: 104 Size of all the elements: 112 Total size of list, including elements: 216 Emtpy list size: 72
We can conclude from this that for every new element, we need another eight bytes for the reference to the new object. The new integer object itself consumes 28 bytes. The size of a list "lst" without the size of the elements can be calculated with:
64 + 8 * len(lst)
To get the complete size of an arbitrary list of integers, we have to add the sum of all the sizes of the integers.
We will examine now the memory consumption of a numpy.array. To this purpose, we will have a look at the implementation in the following picture:
We will create the numpy array of the previous diagram and calculate the memory usage:
a = np.array([24, 12, 57])
print(size(a))
OUTPUT:
120
We get the memory usage for the general array information by creating an empty array:
e = np.array([])
print(size(e))
OUTPUT:
96
We can see that the difference between the empty array "e" and the array "a" with three integers consists in 24 Bytes. This means that an arbitrary integer array of length "n" in numpy needs
96 + n * 8 Bytes
whereas a list of integers needs, as we have seen before
64 + 8 len(lst) + len(lst) 28
This is a minimum estimation, as Python integers can use more than 28 bytes.
When we define a Numpy array, numpy automatically chooses a fixed integer size. In our example "int64". We can determine the size of the integers, when we define an array. Needless to say, this changes the memory requirement:
a = np.array([24, 12, 57], np.int8)
print(size(a) - 96)
a = np.array([24, 12, 57], np.int16)
print(size(a) - 96)
a = np.array([24, 12, 57], np.int32)
print(size(a) - 96)
a = np.array([24, 12, 57], np.int64)
print(size(a) - 96)
OUTPUT:
3 6 12 24
Live Python training
Enjoying this page? We offer live Python training courses covering the content of this site.
Time Comparison between Python Lists and Numpy Arrays
One of the main advantages of NumPy is its advantage in time compared to standard Python. Let's look at the following functions:
import time
size_of_vec = 1000
def pure_python_version():
t1 = time.time()
X = range(size_of_vec)
Y = range(size_of_vec)
Z = [X[i] + Y[i] for i in range(len(X)) ]
return time.time() - t1
def numpy_version():
t1 = time.time()
X = np.arange(size_of_vec)
Y = np.arange(size_of_vec)
Z = X + Y
return time.time() - t1
Let's call these functions and see the time consumption:
t1 = pure_python_version()
t2 = numpy_version()
print(t1, t2)
print("Numpy is in this example " + str(t1/t2) + " faster!")
OUTPUT:
0.0010614395141601562 5.2928924560546875e-05 Numpy is in this example 20.054054054054053 faster!
It's an easier and above all better way to measure the times by using the timeit module. We will use the Timer class in the following script.
The constructor of a Timer object takes a statement to be timed, an additional statement used for setup, and a timer function. Both statements default to 'pass'.
The statements may contain newlines, as long as they don't contain multi-line string literals.
A Timer object has a timeit method. timeit is called with a parameter number:
timeit(number=1000000)
The main statement will be executed "number" times. This executes the setup statement once, and then returns the time it takes to execute the main statement a "number" of times. It returns the time in seconds.
import numpy as np
from timeit import Timer
size_of_vec = 1000
X_list = range(size_of_vec)
Y_list = range(size_of_vec)
X = np.arange(size_of_vec)
Y = np.arange(size_of_vec)
def pure_python_version():
Z = [X_list[i] + Y_list[i] for i in range(len(X_list)) ]
def numpy_version():
Z = X + Y
#timer_obj = Timer("x = x + 1", "x = 0")
timer_obj1 = Timer("pure_python_version()",
"from __main__ import pure_python_version")
timer_obj2 = Timer("numpy_version()",
"from __main__ import numpy_version")
for i in range(3):
t1 = timer_obj1.timeit(10)
t2 = timer_obj2.timeit(10)
print("time for pure Python version: ", t1)
print("time for Numpy version: ", t2)
print(f"Numpy was {t1 / t2:7.2f} times faster!")
OUTPUT:
time for pure Python version: 0.0021230499987723306 time for Numpy version: 0.0004346180066931993 Numpy was 4.88 times faster! time for pure Python version: 0.003020321993972175 time for Numpy version: 0.00014882600225973874 Numpy was 20.29 times faster! time for pure Python version: 0.002028984992648475 time for Numpy version: 0.0002098319964716211 Numpy was 9.67 times faster!
The repeat() method is a convenience to call timeit() multiple times and return a list of results:
print(timer_obj1.repeat(repeat=3, number=10))
print(timer_obj2.repeat(repeat=3, number=10))
OUTPUT:
[0.0030275019962573424, 0.002999588003149256, 0.0022120869980426505] [6.104000203777105e-05, 0.0001641790004214272, 1.904800592456013e-05]
Live Python training
Enjoying this page? We offer live Python training courses covering the content of this site.
Upcoming online Courses